Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков помогает сэкономить время на уроке, успешно сдать экзамен как в 9-м, так и в 11-м классе по математике.
Числа палиндромы и репьюниты образуют одно из наиболее интересных подмножеств множества натуральных чисел. Они обладают необычной историей, удивительными свойствами.
Было проведено исследование среди 7, 8, 9, 11 классов и выяснилось, что многие ребята слышали об этих числах, но подробную информацию знают единицы. Многие из опрошенных учащихся хотели бы узнать об этих числах больше.
В настоящее время при переходе на новые стандарты меняются цели основного и среднего (полного) образования. Одна из главных задач, стоящих перед нами, учителями, в условиях модернизации образования – вооружить учащихся осознанными, прочными знаниями, развивая их самостоятельное мышление. В условиях развития новых технологий возрос спрос на людей, обладающих нестандартным мышлением, умеющих ставить и решать новые задачи. Поэтому в практике работы современной школы все большее распространение приобретает исследовательская деятельность учащихся как образовательная технология, направленная на приобщение учащихся к активным формам получения знаний. Научно-исследовательская деятельность является:
1) мощным средством, позволяющим увлечь новое поколение по самому продуктивному пути развития и совершенствования;
2) одним из методов повышения интереса и соответственно качества образовательного процесса.
Цель: познакомиться с числами палиндромами и репьюнитами и выявить эффективность их применения для обучения современных школьников. Практически все математические понятия, так или иначе, опираются на понятие числа, а конечный результат любой математической теории, как правило, выражается на языке чисел. Многие из них, особенно натуральные числа по тем или иным признакам и свойствам сгруппированы в отдельные структуры (совокупности) и имеют собственные имена.
Задачи:
- раскрыть историю возникновения счета;
- рассмотреть некоторые приемы устных вычислений и на конкретных примерах показать преимущества их использования;
- изучить литературу по теме исследования;
- рассмотреть свойства палиндромов и репьюнитов;
- установить связь между палиндромами и репьюнитами;
- выяснить, какую роль играют простые числа в изменении свойств заинтересовавших нас чисел.
Гипотеза: если использовать нестандартные приемы вычислений , то скорость вычислений увеличивается, а количество ошибок уменьшается.
Простые числа – это часть чисел, из которых состоят все натуральные числа.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
Предмет исследования – множество простых чисел.
Объект исследования –числа палиндромы и репьюниты.
Методы исследования:
- теоретический
- анкетирование
- анализ
Практически все математические понятия, так или иначе, опираются на понятие репьюнитов, а конечный результат любой математической теории, как правило, выражается на языке чисел.
Работа посвящена изучению удивительных чисел: палиндромов и репьюнитов, установлению связи между ними.
1. Палиндромы
История теперь палиндрома насчитывает примерно два тысячелетия. Определено другое название – квадропалин. Палиндром – свойство фракталов, кристаллов и живой материи. Способность самокопирования лежит в человеческой природе глубоко, на генетическом уровне. Молекулы ДНК обнаруживают палиндромные элементы. Сам человек являет собой наглядный пример палиндрома, точнее, частный случай вертикальной симметрии.
Есть такие удивительные фразы, которые читаются одинаково и слева направо, и справа налево. Когда я читала книгу Алексея Константиновича Толстого «Буратино», то обратила свое внимание на такую фразу: А роза упала на лапу Азора. Именно ее просила написать в диктанте неуча Буратино капризная Мальвина.
Называются такие взаимообратные фразы палиндромами, что в переводе с греческого означает «бегущий назад, возвращающийся». Палиндром – одна из древнейших форм литературных экспериментов. Изобретение европейских палиндромов приписывается греческому поэту Сотаду (300 г. до н.э.).
Известен греческий палиндром, вырезанный на купели византийского храма Софии в Константинополе: niyon anomhmata mh monan oyin (омывайте дущу так же как и тело). Здесь уже проявляется заговорный характер палиндрома – записанная по кругу надпись должна служить заклятием от злых сил, не допуская их к святой купели.
Вот некоторые палиндромные фразы: Аргентина манит негра. Умер, и мир ему. Лезу на санузел. У дуба буду. Oколо Миши молоко. Вот сила типа капиталистов. Ешь немытого ты меньше! Откопать тапок-то? «Пустите!» – Летит супу миска Максиму. – «Пустите, летит суп!» Я не реву – уверен я. А муза рада музе без ума да разума. Кулинар, храни лук. Ты, милок, иди яром: у дороги мина, за дорогой огород, а за ним и город у моря; иди, коли мыт. Он в аду давно. Ого, вижу живого.
Меня заинтересовал вопрос. Интересно, есть ли палиндромы в математике? И можно ли перенести эту же идею – идею взаимообратного, симметрического прочтения – в математику. Симметрия (греч.) – соразмерность, одинаковость в расположении частей. Симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали. Многие объекты живой природы, например лист, снежинку, бабочку объединяет то, что они симметричны. Если их мысленно сложить вдоль начерченной прямой, то их половинки совпадут. А если поставить зеркальце вдоль прочерченной линии, то отраженная в нем половинка фигуры дополнит ее до целой. Поэтому такая симметрия называется зеркальной. Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Ежедневно каждый из нас по несколько раз в день видит свое отражение в зеркале. Это настолько обычно, что мы не удивляемся, не задаём вопросов, не делаем открытий. И только философы и математики не теряют способности удивляться.
Что же меняется в предмете при его отражении в зеркале? Мы провели опыты с зеркалами. Если поставить зеркало сбоку от буквы А, то увидим в зеркале ту же самую букву. Но если поставить зеркало снизу, отражение уже не похоже на А – это А вверх дном. А вот если поставить зеркало снизу буквы В, отражение выглядит так же. Зато поставив зеркало сбоку от нее, получим В задом наперед.
Буква А имеет вертикальную симметрию, а буква В – горизонтальную. Итак, мы выяснили, что зеркальная симметрия меняет местами верх-низ, лево-право. Оказывается и среди чисел есть палиндромы. Найти числа-палиндромы в математике не составило труда. Я попыталась составить запись числа для этих чисел-палиндромов.
yy - в двузначных числах-палиндромах число единиц совпадает с числом десятков.
xax – в трехзначных числах-палиндромах число сотен всегда совпадает с числом единиц.
xaax - в четырехзначных числах-палиндромах число единиц тысяч совпадает с числом единиц, а число cотен с числом десятков и т.д.
Палиндромные формулы вызвали у меня больший интерес. Под формулами-палиндромами понимают выражение, состоящее из суммы или разности чисел, результат которого не меняется в результате прочтения выражения справа налево.
Если сложить числа-палиндромы, то сумма не меняется.
Например: 22 + 66 = 66 + 22.
В общем виде это можно записать так:
xx+yy=yy+xx
Задача 1. Найти все пары таких двузначных чисел, чтобы результат их сложения не менялся в результате прочтения суммы справа налево, например, 42 + 35 = 53 + 24.
Запишем равенство:
x1y1+x2y2=y2x2+y1x1.
Представим наши числа в виде суммы разрядных слагаемых:
(10х1 + у1) + (10х2 + у2) = (10у2 + х2) + (10у1 + х1)
10х1 + у1 + 10х2 + у2 = 10у2 + + х2+ 10у1 + х1.
Слагаемые с х перенесем в левую часть равенства, а с у – в правую:
10х1 – х1 + 10х2 – х2 = 10у1 – у1 + 10у2 – у2.
Применим распределительное свойство:
9 х1 + 9 х2 = 9 у1 + 9 у2
9(х1 + х2) = 9(у1 + у2)
х1 + х2 = у1 + у2.
То есть для решения нашей задачи сумма первых цифр должна быть равна сумме их вторых цифр.
Теперь можно составлять такие суммы:
76 + 34 = 43 + 67
25 + 63 = 36 + 52 и т.д.
Задача 2. Найти все пары таких двузначных чисел, чтобы результат их вычитания не менялся в результате прочтения разности справа налево.
x1y1-x2y2=y2x2-y1x1
Представив наши числа в виде суммы разрядных слагаемых и выполнив нужные преобразования, получим, что для решения нашей задачи у таких чисел должны быть равны суммы цифр.
(10х1 + у1) – (10х2 + у2) = (10у2 + х2) – (10у1 + х1)
10х1 + у1 – 10х2 – у2 = 10у2 + х2 – 10у1 – х1
10х1 + х1 + у1 + 10у1 = 10у2 + у2 + 10х2 + х2
11 х1 + 11 у1 = 11х2 + 11у2
11(х1 + у1) = 11(х2 + у2)
х1 + у1 = х2 + у2
Теперь можно составлять такие разности:
41 – 32 = 23 – 14
46 – 28 = 82 – 64
52 –16 = 61 – 25 и т.д.
В случае умножения имеем: 63 • 48 = 84 *36, 82 • 14 = 41 • 28, ... – при этом произведение первых цифр у чисел N1 и N2 равно произведению их вторых цифр (x1 • x2 = y1 • y2).
Наконец, для деления сделать получаем опыт такие примеры: 82/41=28/14; 62/31=26/13 и т.д.
В этом случае произведение первой цифры числа N1 на вторую цифру числа N2 равно произведению двух других их цифр, т.е. x1 • y2 = x2 • y1.
Я попыталась доказать формулу-палиндром для произведения. Вот что у меня получилось.
N1 = x1y1 = 10х1 + у1 N3 = y2x2= 10у2 + х2
N2 = x2y2 = 10х2 + у2 N4 = y1x1 = 10у1 + х1
N1 • N2 = x1y1·x2y2 = (10х1 + у1) • (10х2 + у2)
N3 • N4 = y2x2 · y1x1 = (10у2 + х2) • (10у1 + х1)
100 х1•х2 + 10х1•у2 + 10у1•х2 + у1•у2 = 100у1•у2 + 10х1•у2 + 10у1•х2 + х1•х2
99х1•х2 = 99у1•у2; х1•х2 = у1•у2, что и требовалось доказать.
С помощью понятий числа – палиндром и формулы-палиндромы можно решать задачи на делимость чисел, которые часто встречаются в олимпиадах по математике. Вот одна из них:
Задача. Докажите, что если из трехзначного числа вычесть число, записанное теми же цифрами, но в обратном порядке, разность будет делиться на 9.
Решение.
abc–cba=100a+10b+c–(100c+10b+a)= 100a+10b+c–100c–10b–a=99a–99c=99(a–c)=9·11(a–c), т.е. данное произведение всегда делится класса на 9.
Между прочим, превращается нашему поколению выпала большая удача, не каждому человеку выпадает прожить хотя бы один палиндромный год, а уж тем более два – 1991-й и 2002-й.Ведь предыдущий был в 1881-м, а следующий – в 2112-м. В своей работе мы прикоснулись к удивительному математическому явлению – симметрии, в частности к ее проявлению – палиндромам.
В своей работе я рассмотрела числа-палиндромы, формулы-палиндромы для суммы и разности, произведения и частного двузначных чисел и смогла их доказать. Путь познания законов гармонии и красоты долог и труден, и мы находимся только в его начале.
Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Иначе говоря, отличаются симметрией записи (расположения цифр), причём число знаков может быть как четным, так и нечётным.
Например: 121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.
Изучая палиндромы, автор данной работы задает вопрос: «Как из других чисел можно получить палиндромы?»
Палиндром можно получить как результат операций над другими числами. Для этого воспользуемся известным алгоритмом.
Алгоритм получения палиндрома:
- Возьми любое двузначное число
- Переверни его (переставь цифры справа налево)
- Найди их сумму
- Переверни полученное число
- Найди их сумму
- Повторяй аналогичные действия до тех пор, пока не получится палиндром
Пример:
a) 96
b) 96 + 69 = 165
c) 165 + 561 = 726
d) 726 + 627 + 1353
e) 1353 + 3531 + 4884
В результате проделанной работы я пришла к выводу, что, используя составленный алгоритм, из любого двузначного числа можно получить число-палиндром.
Можно рассмотреть не только сложение, но и другие операции над палиндромами (прил. 2).
Приведем два примера того , как при помощи одних палиндромов получаются другие:
а) 212 ² – 121 ² = 44944 – 14641 = 30303;
б) 2·121·10201 = 2·11 ² ·101 ² = 22·112211= = 1111· 2222 = 2468642.
Теперь обратимся к числам простым. В их бесконечном множестве имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причем двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11. С такими числами связано немало интересных закономерностей:
O Существует единственный простой палиндром с четным числом цифр – 11.
O Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары.
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97.
O Среди простых трехзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.
O Аналогичная картина наблюдается у больших простых чисел.
Например: 94849 и 94949; 1177711 и 1178711.
O Все однозначные числа являются палиндромами.
O 26 – наименьшее число, не являющееся палиндромом, квадрат которого палиндром
Например: 26 ² = 676
O А вот пары чисел – «перевертышей» 13 – 31 и 113 – 311 при возведении в квадрат дают также пары «перевёртышей»: 169 – 961 и 12769 – 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1+3)2=1+6+9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
O Из простых чисел-палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
Таблица 1
Примеры палиндромов
|
В русском языке |
Утречко летело к черту Я ем змея Я нем и нежен, не жени меня Я ужру буржуя! Нам рак влетел в карман Цени в себе свинец |
|
Магический квадрат |
|
|
В биологии |
Палиндромы в ДНК 1 – палиндром |
|
В химии |
НООССООН – формула щавелевой кислоты |
|
В изобразительном искусстве |
|
|
В пространственной математике Лента Мебиуса |
|
2 Репьюниты
Репьюниты – натуральные числа, запись которых состоит только из единиц. В десятичной системе счисления репьюниты обозначаются короче Rn: R1 = 1, R2 = 11, R3 = 111 и т. д., и общий вид для них:
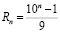, n= 1, 2, 3…
Общий вид репьюнита может быть записан в другом виде:
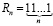
Например: 11; 111; 1111; 11111; 111111; 1111111 и т. д.
Обнаружено немало интересных свойств репьюнитов:
O Репьюниты – частный случай чисел-палиндромов, которые остаются неизменными при прямом и обратном прочтении.
O Репьюниты относятся к таким палиндромам, которые делятся на произведение своих цифр.
O Известно пять простых репьюнитов: R2, R19, R23, R317 и R1031, причем, что самое интересное – индексы этих репьюнитов также простые числа. Самое маленькое число репьюнит – 1. Самое большое – еще не найдено.
O В семействе репьюнитов выявлено пока только 9 простых чисел: 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343 (индексы репьюнитов).
O Раскладывая некоторые составные репьюниты на простые множители:
111 = 3•37
1111 = 11•101
11111 = 41• 271
111111 = 3•7•11•13•37
1111111 = 239•4649
11111111 = 11•73•101•137
111111111 = 3•37•333667 и т. д. можно заметить числа палиндромы.
O В результате умножения некоторых репьюнитов мы получили числа-палиндромы:
11•11 = 121
11•111 = 1221
1111•11 = 12221
111•111 = 12321
11111•111 = 1233321
11111•1111 = 12344321
11111•11111 = 123454321 и т.д.
Перемножив немало репьюнитов, можно сделать вывод о том, что каждый раз получается число-палиндром (прил. 3).
Число 7 – особенное, т.к. его запись по основанию 2: 111, а по основанию 6: 11 (т.e. 710 = 116 = 1112).
Другими словами, число 7 является репьюнитом по крайней мере в двух основаниях b > 1.
Определим положительное целое число с таким свойством как сильный репьюнит. Можно убедиться, что существует 8 сильных репьюнитов меньше 50: {1,7,13,15,21,31,40,43}.
Далее, сумма всех репьюнитов меньше 1000 равна 15864.
Таблица 2
Пример репьюнита
|
В математике
|
Треугольник, полученный из исходного после добавления к нему шести простых палиндромов. Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Ее окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и еще столько же – «боковые стороны» треугольника. |
В других областях науки примеры репьюнитов не найдены.
Практическая часть
Решим две интересные задачи из журнала «Квант» №5 за 1997 год.
Задача №1
Какими цифрами следует заменить буквы, чтобы сумма девяти слагаемых стала равной репьюниту?
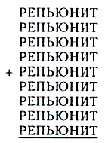
Решение: 12345679+12345679+12345679+12345679+12345679+12345679+12345679+ +12345679+12345679=111111111 – репьюнит
Ответ: 111111111
Задача №2
Произведением каких двух репьюнитов является число 123455554321?
Решение.
Перемножив два репьюнита, мы получили:
11111111 · 11111 = 123455554321.
Ответ: 11111111 · 11111
Прослеживается закономерность: цифры в записи упорядочены сначала по возрастанию, а затем по убыванию, причем наибольшей цифрой является длина меньшего репьюнита, а количество повторений этой цифры в середине числа равно разности длин репьюнитов, увеличенной на единицу. Перемножив немало репьюнитов, делаем вывод о том, что каждый раз получается число-палиндром (Прил. 3).
Также экспериментально доказано, что при перемножении репьюнитов, если по правилу, наименьшее число единиц должно быть меньше 10. То есть максимальное произведение единиц: 1(19 раз) * 1(9 раз)= 1 234 567 899 999 999 999 987 654 321. Далее палиндром не получается.
Решение занимательных и олимпиадных задач
Вычислительный аппарат
1) 
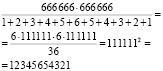
Ответ: 12 345 654 321
2) 
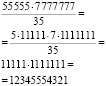
Ответ: 12 345 554 321
Задача 1.
Вычислить количество чисел-палиндромов, делящихся на 2:
а) двузначных
б) трехзначных
в) четырехзначных
г) пятизначных
Ответ.
На 2 делится любое четное число. Поэтому:
а) среди двузначных чисел-палиндромов четные – 22, 44, 66 и 88. То есть 4 числа.
б) у трехзначных чисел-палиндромов первая и последняя цифры одинаковые и должны быть четными. Четных цифр 4 (2, 4, 6 и 8). В середине может стоять любая из 10 цифр от 0 до 9. Поэтому, всего 4*10=40 трехзначных чисел-палиндромов.
в) у четырехзначного искомого числа должны быть четными одинаковые первая и последняя цифры – их 4. При этом одинаковые вторая и третья цифры могут быть любыми из десяти. Значит, четырехзначных чисел-палиндромов тоже 40.
г) у пятизначных чисел-палиндромов первая и последняя цифры одинаковы и четны, их может быть 4. При этом 2 и 4 цифры также одинаковы и их может быть 10. Третья цифра также может быть любой из 10. Поэтому всего пятизначных чисел-палиндромов – 4*10*10=400.
Итак, все мы убедились в том, что математика важна не только сама по себе. Математический подход к окружающему миру помогает лучше его познать. И математический стиль мышления нужен сегодня всем – и языковеду, и биологу, и химику, и физику, и инженеру, и художнику, и поэту, и музыканту.
Проведя исследование по данной теме, я изучила свойства палиндромов и репьюнитов, установила связь между ними, выяснила какую роль играют простые числа в изменении свойств данных чисел.
Результаты исследования (сходство и различие) занесены в таблицу.
Таблица 3
Сравнение свойств палиндромов и репьюнитов
|
Категории сравнения |
Палиндромы |
Репьюниты |
|
Читается слева направо и справа налево одинаково |
+ |
+ |
|
Симметрия записи (расположения цифр) |
+ |
- Не всегда |
|
Число знаков, используемых при записи чисел, может быть четным и нечётным |
+ |
+ |
|
Можно получить как результат операций над другими числами: - сложение - возведение в степень - извлечение корня - умножение |
+ + + + |
+ + + + |
|
Можно получить многоугольные фигуры |
+ |
+ |
|
Являются представителями класса простых чисел |
+ |
+ |
Результаты опроса
Таблица 4
Хотите ли знать больше об этих числах?
|
Палиндромы |
Репьюниты |
||||||||
|
Классы |
Кол-во учащихся |
Хотите узнать больше об этих числах? |
|||||||
|
Да |
% |
нет |
% |
да |
% |
нет |
% |
||
|
7а |
31 |
31 уч. |
100 |
0 уч. |
0 |
31 уч. |
100 |
0 уч. |
0 |
|
8в |
29 |
29 уч. |
100 |
2 уч. |
0 |
29 уч. |
100 |
2 уч. |
0 |
|
9а |
26 |
26 уч. |
100 |
0 уч. |
0 |
26 уч. |
100 |
0 уч. |
0 |
|
11б |
23 |
23 уч. |
100 |
0 уч. |
0 |
23 уч. |
100 |
0 уч. |
0 |
Результаты опроса показали, что все учащиеся хотят знать больше о числах-палиндромах и репьюнитах.
Также провела опрос «Используете ли вы эти числа в жизни?». Данные занесла в таблицу.
Таблица 5
Используете ли вы эти числа в жизни?
|
Классы |
Кол-во учащихся |
Используете ли вы эти числа в жизни? |
|||
|
Да |
% |
нет |
% |
||
|
7а |
31 |
15 уч. |
48 |
16 уч. |
0 |
|
8в |
29 |
17 уч. |
58 |
19 уч. |
0 |
|
9а |
26 |
20 уч. |
76 |
6 уч. |
0 |
|
11б |
23 |
19 уч. |
82 |
4 уч. |
0 |
Выводы по опросу: Чем старше школьник, тем он чаще использует палиндромы и репьюниты в воей жизни.
Приложение 1
Операции над палиндромами
|
Число |
Действие |
Результат |
Полученное число |
|
17 |
17 + 71 |
88 |
Палиндром |
|
132 |
132 + 231 |
363 |
Палиндром |
|
111 |
111 ² |
12321 |
Палиндром |
|
111111111 |
111111111 |
12345678987654321 |
Палиндром |
|
1 |
1·1 |
1 |
Палиндром Репьюнит |
|
1 |
v1 |
1 |
Палиндром Репьюнит |
|
121 |
v121 |
11 |
Палиндром Репьюнит |
Выполняя действия над палиндромами в результате можно получить и палиндром, и репьюнит.
Приложение 2
Произведение репьюнитов дает палиндром.
|
1 множитель |
2 множитель |
Произведение |
|
111 |
111 |
12321 |
|
111 |
1111 |
123321 |
|
111 |
11111 |
1233321 |
|
111 |
111111 |
12333321 |
|
1111 |
1111 |
1234321 |
|
1111 |
11111 |
12344321 |
|
1111 |
111111 |
123444321 |
|
11111 |
11111 |
123454321 |
|
11111 |
111111 |
1234554321 |
|
111111 |
111111 |
12345654321 |
|
111111 |
1111111 |
123456654321 |
|
1111111 |
11111111 |
1234567654321 |
|
11111111 |
111111111 |
1234567887654321 |
|
111111111 |
1111111111 |
12345678887654321 |
|
1111111111 |
111 |
123333333321 |
|
11111111111 |
1111 |
12344444444321 |
|
1111111111111 |
111 |
123333333333321 |
|
11111111111111 |
11 |
122222222222221 |
|
111111111111111 |
111 |
12333333333333321 |
Перемножив немало репьюнитов, делаем вывод о том, что каждый раз получается число палиндром.
Приложение 3
Приложение 4
Фото опыта
Заключение
Мир чисел настолько загадочен и увлекателен, что занимаясь данной работой, исследовано, что если бы каждый из нас уделял ему больше внимания, то нашел бы для себя много нового и интересного, познакомившись с удивительными натуральными числами: палиндромами и репьюнитами. Все они обязаны своими свойствами простым числам.
Значит, подтверждена гипотеза о том, что простые числа – это часть чисел, из которых состоят все натуральные числа.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
В своей работе большое внимание уделяю проектам, имеющим конкретное общественно-полезное значение. Часто эти проекты являются долгосрочными, ориентированными на создание системы: урок – внеклассная деятельность.
Организационно метод проектов предусматривает сочетание индивидуальной самостоятельной работы с работой в сотрудничестве, в малых группах и в коллективе. Реализация метода проектов на практике ведет к изменению позиции учителя. Из носителя готовых знаний он превращается в организатора познавательной, исследовательской деятельности своих учеников. Изменяется и психологический климат в классе, так как учителю приходится переориентировать свою учебно-воспитательную работу и работу учащихся на разнообразные виды самостоятельной деятельности, на приоритет деятельности исследовательского, поискового, творческого характера. Обеспечение и сопровождение проектной деятельности строится на принципах сотрудничества и включает:
a) помощь в определении школьником замысла проектной деятельности;
b) консультирование стадий проекта: поиска информации, решений проектных задач, поощрение практического опыта непосредственной работы с текстом;
c) внимание к индивидуальным формам и способам аналитического и образного мышления, рассуждений и интерпретации, инициирование навыков продумывания деятельности и прогнозирования ее продукта;
d) поощрение инициативы и творческого характера проектной деятельности;
e) участие в обеспечении презентации и общественной экспертизы результатов проектной деятельности детей.
В результате активного внедрения метода проектов на уроках и во внеурочной деятельности теперь у учащихся формируются общие учебные умения, навыки и обобщенные способы деятельности. Обучающиеся более прочно усваивают знания, полученные в ходе самостоятельного решения поставленных задач. Ученики приобретают опыт вдумчивой работы с текстом художественного произведения, опыт работы с большим объемом информации из различных источников. Школьники приобретают навыки учебного сотрудничества и коммуникации: учатся чего работать в коллективе, планировать работу индивидуально и в группе, учатся оценивать ситуации и принимать решения.
Проектная деятельность на уроке и во внеурочное время способствует формированию у школьников духовности и культуры, инициативности, самостоятельности, способности к успешной социализации в обществе и активной адаптации на рынке труда.
Метод проектной деятельности актуален в связи с изменениями, происходящими в образовании. Компьютеры и мультимедиа стали неотъемлемой частью образовательного пространства. В работе использую компьютер как необходимое условие проведения современного урока. Сегодня техника позволяет представлять результаты своей деятельности ярко, логично, подбирать систему доказательств, иллюстраций к основным вопросам темы.
В процессе работы над проектом с использованием средств ИКТ формируется человек, умеющий действовать не только по образцу, но и самостоятельно, получающий необходимую информацию из максимально большего числа источников, умеющий ее анализировать и делать выводы. Метод проектов востребован школой, так как он демонстрирует высокую эффективность, мотивированность обучения, снижение перегрузки, повышение творческого потенциала учащихся.
Библиографическая ссылка
Сурова А.А. ПАЛИНДРОМЫ И РЕПЬЮНИТЫ // Международный школьный научный вестник. – 2018. – № 4-3. ;URL: https://school-herald.ru/ru/article/view?id=616 (дата обращения: 23.11.2024).