Международный школьный научный вестник

Научный журнал для старшеклассников и учителей ISSN 2542-0372

• Авторы
• Научный руководитель
• Файлы
• Литература

Талханов Д.А. 1

---

1 г. Владикавказ, МБОУ «СОШ № 30», 8 «А» класс

Караева Д.А. (Владикавказ, МБОУ «СОШ № 30»)

Статья в формате PDF

1493 KB

1. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971. – 511 с.

2. Дьюдени Г.Э. Кентерберийские головоломки. – М.: Мир, 1979. – 353 с.

3. Дьюдени Г.Э. 520 головоломок. – М.: Мир, 1975. – 342 с.

4. Перельман Я.И. Веселые задачи. – М.: АСТ, 2003. – 287 с.

5. Перельман Я.И. Головоломки. Задачи. Фокусы. Развлечения. – М.: АСТ, 2015. – 192 с.

6. Перельман Я.И. Живая математика. – М.: Наука, 1978. – 160 с.

Предмет исследования: структура математических объектов.

Объект исследования: математические головоломки.

Цель исследования: выявить скрытую структуру исследуемого объекта.

Задачи исследования:

– изучить существующие виды математических головоломок;

– рассмотреть различные виды математических объектов с точки зрения их решения.

Методологическую базу составили головоломки, предложенные математиками и составителями головоломок Генри Э. Дьюдени, Мартином Гарднером, Яковом Перельманом.

Когда мы решаем какие-либо нестандартные и уникальные задачи, мы подсознательно ощущаем величие математики. Было бы ошибочным считать решение задач скучным и неинтересным занятием. В математике головоломки не являются пустой забавой. Иногда они приводят к глубоким открытиям, сделанным учеными в различных областях науки.

Из-за ограничения во времени, программа средней школы не позволяет подробно останавливаться на решении задач подобного рода, хотя именно занимательная математика учит наблюдательности, умению мыслить логически и способности воспринимать окружающий мир во всем его многообразии. Поэтому, мы посчитали необходимым, еще раз, обратиться к исследованию увлекательного мира математических головоломок. Этот мир настолько разнообразен, что в небольшой исследовательской работе не представляется возможным подробно рассмотреть все существующие виды математических головоломок. В связи с чем, мы рассматривали только те виды головоломок, которые связаны с такой геометрической фигурой как квадрат.

Основная часть

Квадраты в головоломках со спичками

Головоломки со спичками можно часто встретить в учебниках математики начальной школы, и, как правило, они оказываются не такими уж сложными. Задачи посложнее предлагаются для взрослых, и прекрасно развивают логику и творческое мышление. Их удобно решать, т.к. всегда есть наглядное пособие, в виде спичек, и можно подбирать разные варианты составления геометрических и арифметических фигур.

Известные задачи со спичками, предложенные Я.И. Перельманом.

В представленной на рис. 1 решетке из спичек, нужно убрать:

а) «4 спички, чтобы получилось 5 квадратов». [4, с. 176–179];

Рис. 1

Решение представлено на рис. 2.

Рис. 2.

б) «8 спичек, чтобы получилось 4 квадрата (возможно два решения)». [4, с.176–179];

Решение представлено на рис. 3.

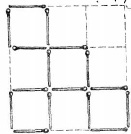
Рис. 3

в) «6 спичек, не перекладывая остальных, чтобы осталось всего 3 квадрата». [4, с.176–179]

Решение представлено на рис. 4.

г) «8 спичек, чтобы осталось два квадрата». [4, с.176–179]

Решение представлено на рис. 5.

Рис. 4

Рис. 5

Квадраты в головоломках с домино

Квадраты встречаются также в головоломках из домино. Г. Дьюдени предлагает следующие головоломки.

Полые квадраты из домино. «Надо составить 7 полых квадратов из 28 костяшек домино (похожих на квадрат, изображенный на рис. 6), так, чтобы в любом квадрате суммы очков вдоль каждой из сторон равнялись между собой. У всех 7 квадратов общие суммы очков не обязаны совпадать. Данный квадрат может не входить в множество из 7 квадратов» [3, с. 193–194].

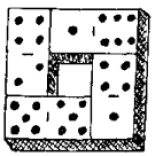
Рис. 6

«Составить 6 квадратов разными способами несложно, но, при попытке сложить из оставшихся четырех костяшек седьмой квадрат могут возникнуть трудности». [3, с. 193–194]

Решение: Как видно из рис. 7 «можно сложить из 28 костяшек 7 полых квадратов, чтобы при этом суммы очков вдоль каждой из сторон в любом квадрате равнялись между собой. При составлении квадратов нужно учесть, что если сумма очков равна, например, 7, а надо, чтобы их сумма вдоль каждой из сторон равнялась 3, то 4 3 – 7 дает нам 5 – сумму очков в четырех углах. Так, в последнем примере 4 16 = 64 -43 говорит о том, что сумма очков, стоящих по углам, должна равняться 21, что и есть на самом деле» [3, с. 330].

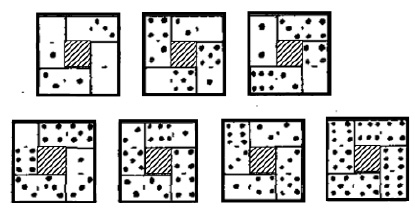
Рис. 7

Квадраты из домино. Составьте из 28 костяшек домино 2 квадрата, как показано на рис. 8, «чтобы суммы очков вдоль каждой из 8 сторон совпали. Значение сумм должно быть таким, чтобы головоломка оказалась разрешимой. Не обязательно прикладывать костяшки друг к другу согласно обычному правилу – 5 к 5, 1 к 1 и т. д». [3, с. 194]

Решение. На рис. 9 показано, как можно составить из 28 костяшек два квадрата, «у которых сумма очков вдоль любой из сторон равна 22. Если сумма равна 22, то сумма углов должна равняться 8; если 23, то 16; если 24, то 24; если 25, то 32; если 26, то 40. Сумма не может быть меньше 22 или больше 26» [3, с.3 30].

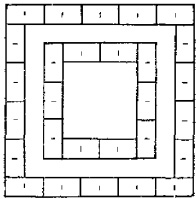
Рис. 8

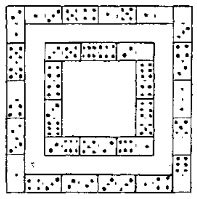
Рис. 9

Магические квадраты

В современных учебниках математики, как задачи повышенной трудности, предлагаются, так называемые магические квадраты.

Магический квадрат – это квадратная таблица, n×n (n – число строк), в которой сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой – М.

«Число клеток, примыкающих к его стороне, называется «порядком» магического квадрата. Магических квадратов порядка 3 существует только один, магических квадратов порядка 4 – 880 типов (если не считать магических квадратов, получающихся из него при поворотах и отражениях) и т.д.» [1, с. 256–257]. Наименьшая магическая константа 3 порядка =15; 4 порядка =34; 5 порядка =65 и т. д.

Примеры магических квадратов:

3-го порядка (М – 66):

Рис. 10

4-го порядка (М – 50):

Рис. 11

5-го порядка (М – 115)

Рис. 12

Интересен квадрат, представленный на рис. 13. В нем, одному и тому же числу, равна сумма не только чисел, стоящих в строках, столбцах и двух диагоналях, но и суммы чисел, стоящих в квадратах из четырех клеток, расположенных по углам и в середине, а также сумма чисел, стоящих в вершинах этого магического квадрата (М – 42).

Рис. 13

Существуют различные методы заполнения магических квадратов. Это можно сделать, вычислив магическую константу. Магическую константу квадрата любого порядка легко вычислить по общей формуле

М= n(n² +1)/2.

Задача: Предлагается заполнить магический квадрат 3 порядка, зная его константу М=30. Мы знаем, что наименьшая магическая константа квадрата 3 –порядка равна 15: М= 3(9 +1)/2=15. Этот квадрат представлен на рис. 14.

Рис. 14

Решение: Вначале найдем число, записанное в центре магического квадрата. Для этого разделим магическую константу на n (число строк): 30/3=10. Затем каждое число искомого квадрата увеличим на 10–5=5. Мы получим следующий квадрат (рис. 15).

Рис. 15

Г. Дьюдени предлагает следующую задачу с магическим квадратом:

«Из девяти цифр, различными способами можно составить квадрат так, чтобы третья строка была суммой чисел первой и второй строк. В трех следующих примерах обнаруживается еще одна закономерность: разность между второй суммой (819) и первой (657) равна разности между третьей суммой (981) и второй (819» (рис. 16) [3, с. 44].

Рис. 16

Задача. Надо составить восемь квадратов (каждый из девяти цифр) так, чтобы разность между соседними суммами была постоянной (эта разность будет отличаться от 162).

Решение. «В каждом из следующих восьми примеров девять цифр используются по одному разу, а разность между соседними суммами равна 9 [3, с. 236].

Следующая головоломка перекликается с приведенными в предыдущей главе примерами головоломок с домино. «На рис. 17 показан магический квадрат из 18 косточек домино. Сумма очков любого его ряда (продольного, поперечного или диагонального) будет 13» [6, с.2 5–26].

Рис. 17

Как составить несколько таких же 18–косточковых магических квадратов, но с другой суммой очков в ряду. Наибольшая сумма в рядах магического квадрата составленного из 18 костей – 23, а наименьшая – 13.

Решение. «На рисунке 18 приводится образец магического квадрата, составленного из 18 костей, с суммою очков в ряду – 18». [6, с. 35–36].

Рис. 18

Головоломки на разрезание бумаги и составление квадратов

Разрезание многоугольников на части и составление из них новых многоугольников относится к числу одних из самых увлекательных задач. Доказано, что любой многоугольник можно разрезать на конечное число частей, образующих любой другой многоугольник, равновеликий первому [1, c. 390].

Головоломка Дьюдени на разрезание. Испорченный крест. «Из симметричного греческого креста (рис. 19) вырезан квадратный кусок, в точности равный одному из концов креста. Оставшуюся часть надо разрезать на четыре куска, из которых можно составить квадрат» [3].

Рис. 19

Решение. Из рис. 20 видно, как нужно разрезать крест на четыре части, чтобы из них можно было составить квадрат. «Надо просто продолжить каждую сторону квадратного отверстия до соответствующего угла» [3].

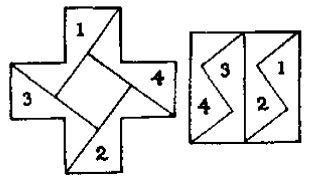
Рис. 20

Я.И. Перельман предлагает следующие головоломки:

Двумя взмахами ножниц. «Крест, изображенный на рис. 21 надо разрезать на четыре части двумя взмахами ножниц, чтобы из них можно было составить сплошной квадрат» [5].

Рис. 21

Решение. «Первым взмахом ножниц отрезаем от креста два крайних кусочка. Вторым – разрезаем на две части оставшийся кусок. На рис. 22 показано, как нужно соединить между собой, полученные четыре кусочка, чтобы получился квадрат» [5].

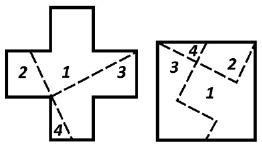
Рис. 22

Из пяти кусочков. Следующая задача (рис. 23) заключается в том, чтобы из пяти кусочков составить квадрат [5].

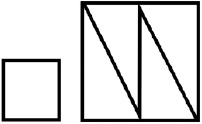
Рис. 23

Решение. Квадрат составляется следующим образом (рис. 24).

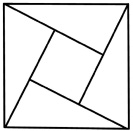
Рис. 24

И, наконец, головоломка, сочетающая в себе и задачу на разрезание, и магический квадрат.

Головоломка с магическим квадратом. Квадрат, представленный на рис. 25 «надо разрезать на четыре части (вдоль прямых), которые можно было бы сложить заново так, чтобы получился правильный магический квадрат. У квадрата, который получится, сумма чисел в каждой строке, столбце и на каждой диагонали должна быть равна 34» [2].

Рис. 25

Решение. На рис. 26 «показано, как надо разрезать квадрат на четыре части и как их сложить, чтобы получился» магический квадрат, с константой 34 [2, с. 229].

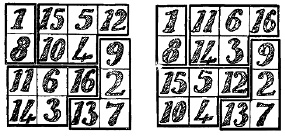
Рис. 26

Заключение

При написании работы по теме исследования была изучена специальная литература, рассматривающая головоломки, предложенные Генри Э. Дьюдени, Мартином Гарднером, Яковом Перельманом.

При решении задач исследования, в работе были проанализированы различные виды головоломок, в частности головоломки со спичками, головоломки с домино, магические квадраты, головоломки на разрезание бумаги. Также были рассмотрены различные виды математических объектов с точки зрения их решения и выявлена скрытая структура исследуемого объекта. Таким образом, задачи, поставленные в исследовании, решены, цель достигнута.

На основании проведённых исследований можно сделать вывод о том, что математические головоломки являются неотъемлемой частью тренировки логического мышления и умения находить нестандартное решение поставленных задач.

Практическая значимость работы заключается в возможности использования предложенных задач для развития логического мышления не только на уроках математики в средней школе, но и в повседневной жизни.

В дальнейшем, нам представляется целесообразным, рассмотреть другие виды геометрических фигур в задачах подобного рода.

Библиографическая ссылка